경희대학교 박제만 교수님의 자료구조 수업을 기반으로 정리한 글입니다.
Recursion
Definitions
- Recursive call: 재귀, 자기 자신을 호출하는 것
Direct recursion: 직접적으로 자기 자신을 호출, e.g., a 함수가 a 함수 호출
Indirect recursion: 다른 함수를 우회해 자기 자신을 호출, e.g., a 함수가 b 함수 호출 -> b가 a 함수 호출
Recursion의 필요성
recursive한 프로그래밍은 모두 nonrecursive한 방법으로도 가능하다.
즉, 반드시 필요한 것은 아니기에 recursion을 사용하지 않아도 모든 알고리즘 구현 가능하다.
Recursive solutions can be less efficient than iterative solutions.
Still, many problems lend themselves to simple, elegant, recursive solutions.
- iterative solutions: for문, while, ...
Recursion vs. Iteration
int fib(int n){
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}▶ Recursion
- time complexity: O(2^N)
※ O(2^N) 시간 복잡도는 사용 불가능한 수준의 안 좋은 시간 복잡도이다.
int fib(int n) {
if (n <= 1)
return n;
int prev2 = 0; // fib(0)
int prev1 = 1; // fib(1)
int cur;
for (int i = 2; i <= n; i++) {
cur = prev1 + prev2;
prev2 = prev1;
prev1 = cur;
}
return cur;
}▶ Iteration
- time complexity: O(N)
위 예시에서 recursion을 사용한 코드가 훨씬 더 직관적이지만 효율성은 iteration을 사용한 코드가 훨씬 더 좋다.
- 항상은 아니지만 일반적으론 iteration이 더 효율적임
Recursion
How Recursion is Defined
- Base (nonrecursive) case: 멈추는 조건 (언제 끝낼지 정의, 종료 조건)
- General (recursive) case: 자기 자신을 호출하는 부분 (작게 나눠서 반복) // 점화식
Recursive algorithm: general case에서 점점 base case에 가깝도록 만들어주는 알고리즘
We must avoid making an infinite sequence of function calls.
Each recursive algorithm must have at least one base case, as well as the general (recursive) case.

▶ General Format
Verifying Recursive Functions
- Base Case Question: base case를 가지고 있는가?
- Smaller-Caller Question: general case에서 base case로 문제가 점점 작아지고 있는가?
Example
Recursive Factorial
For a situation in which the answer is known, the value of 0! is 1.
Now for the general case, the value of Factorial(n) = n * Factorial(n - 1)
- Notice that the recursive call Factorial(n - 1) gets us "closer" to the base case of Factorial(0).

▶ Recursive Factorial
- Time Complexity: O(N) (재귀함수라고 다 N^2 시간 복잡도 아님 주의 -> 코드 잘 보기)

▶ Recursion
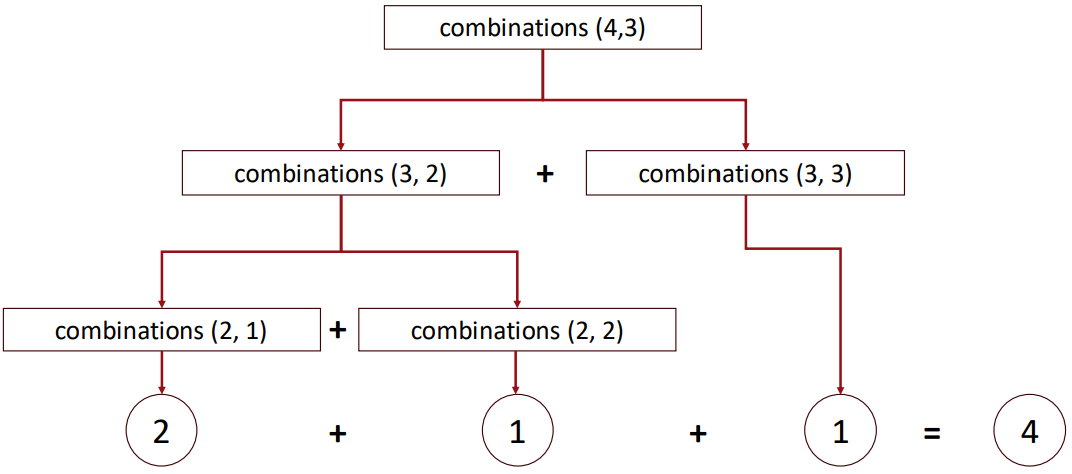
Combinations
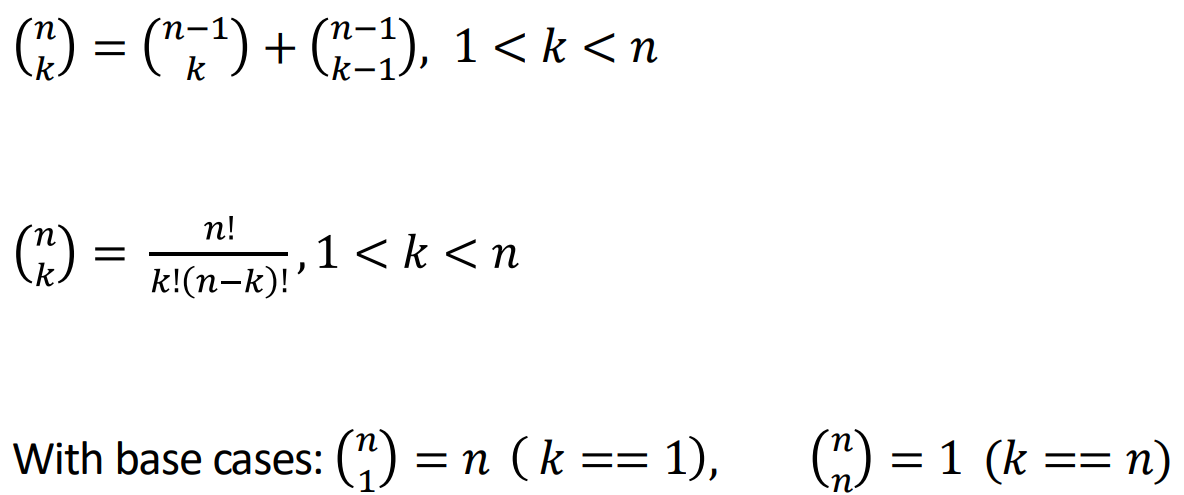
▶ nCk

▶ Combinations
- Time Complexity: O(2^N)
▶ Recursion
x to the power of n

▶ x^n

▶ x to the power of n
- Time Complexity: O(N)
Recursion + ADT
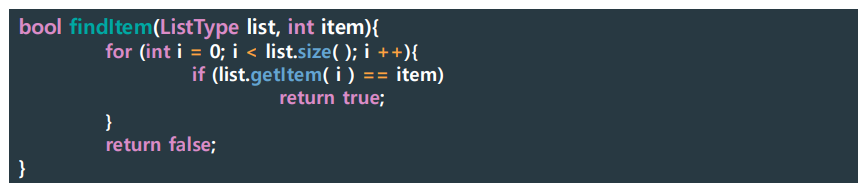
Finding Item in Array
using Iteration
▶ Finding Item in Array using Iteration
Iterative Solution:
We usually implement linear searching using for loop.

▶ code
using recursion
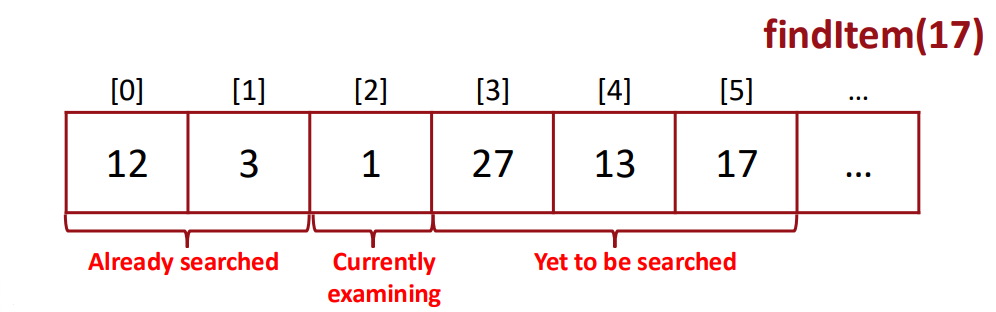
▶ Finding Item in Array using Recursion
Recursive Solution:
We can check one item per recursive function.
How do we set the base cases?
- If the element that is being examined is equal to "item" then true.
- If NOT equal to "item" and it is the last element of the list, then false.

▶ code
If you want to find 17 in the list, just invoke findItem(list, 17, 0).
- Since list.data[0] != 17, it will call findItem(list, 17, 1).
- Since list.data[1] != 17, it will call findItem(list, 17, 2).
- Since list.data[2] != 17, it will call findItem(list, 17, 3).
- Since list.data[3] != 17, it will call findItem(list, 17, 4).
- Since list.data[4] != 17, it will call findItem(list, 17, 5).
- Since list.data[5] == 17, thus it returns true (recursively terminates).
모든 Iteration은 recursion으로 바꿀 수 있고, 반대로 모든 recursion도 Iteration으로 바꿀 수 있다.
Binary Search
using Iteration

▶ code
using recursion

▶ Binary Search using Recursion
Base case:
- If mid == item, then return true;
- If first > last, then return false;
General case:
- If item > mid, search upper half.
- If item < mid, search lower half.

▶ code
- Time Complexity: O(log N)
In general, iterative solutions use loops (for or while statements),
while recursive solutions use branches (if-else statements).
문제에 따라 어떤 거는 iterative가 시간 복잡도 측면에서 유리할 수도, recursion이 유리할 수도,
또 어떤 거는 시간 복잡도가 같을 수도 있다.
하지만 일반적으로는 iterative가 시간 복잡도 측면에서 유리하다. (e.g., 피보나치 수열 O(2^N) vs O(N))
또한, 함수가 호출될 때마다 stack의 function call stack이라는 공간에 activation record가 만들어지기에, (memory overhead)
자기 자신을 계속해서 호출하는 recursion의 경우 stack에 activation record가 계속 쌓여 메모리 사용량 측면에서 비효율적이다..
Why Use Recursion?
Example
RevPrint()

▶ RevPrint() using Recursion
- Print the list in reverse order (D - C - B - A).
Can we implement an iterative solution (using for or while)?
- Maybe YES, but Time Complexity is O(N^2).
- tempPtr을 A부터 D까지, A부터 C까지, ... 이런식으로 끝까지 이동시키고 돌아오고를 반복해야 함 (traverse 반복)
이렇게 pointer 변수가 사용되는 구조에서는 recursion이 필요한 경우들이 있다. (e.g., singly linked structure 역순 print)

▶ RevPrint() using Recursion

▶ RevPrint() using Recursion
- Time Complexity: O(2N) -> O(N)
Other Solution?
- 역순 -> Use STACK!
- Push all items, and then pop and print them one by one!
- Time Complexity: O(N)
InsertItem()

▶ insertItem() using Iteration

▶ insertItem() using Iteration
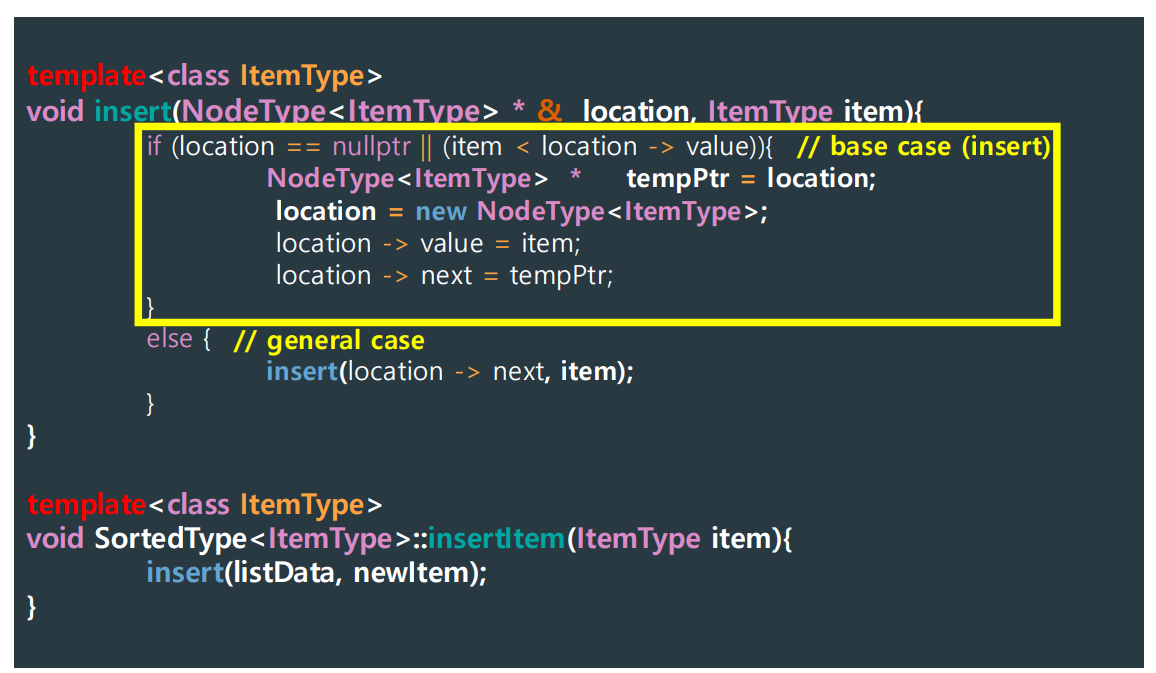
▶ insertItem() using Recursion
- insertItem: recursion 함수인 insert에 대한 인터페이스 함수
- 인터페이스 함수 없이 외부에서 insert를 직접 호출하면 item 값 뿐만 아니라 listData 값도 동시에 주며 호출해야 함
- recursive 함수 / 인터페이스 함수
- location == nullptr: item이 list에 있는 값보다 가장 큰 값일 때 or 리스트가 비어있을 때
이렇게 recursion은 일반적으로 인터페이스 구조를 많이 가진다.
To insert a node into the linked structure list, we updated two pointers:
- PrevNode -> next = NewNode.
- NewNode -> next = NextNode.
In this code, we changed only one pointer (location -> next = tempPtr).
Understanding "NodeType<Item Type> * & location"

▶ What is listData -> next?
- Node B? X
- It means the pointer variable (named "next") in node A.
- Node A's next still means node B!
What's different?

▶ When RevPrint(listPtr) is called:
- Since listPtr != nullptr, it will call RevPrint(listPtr -> next).
- It passes the pointer "listPtr -> next" through a call-by-value.

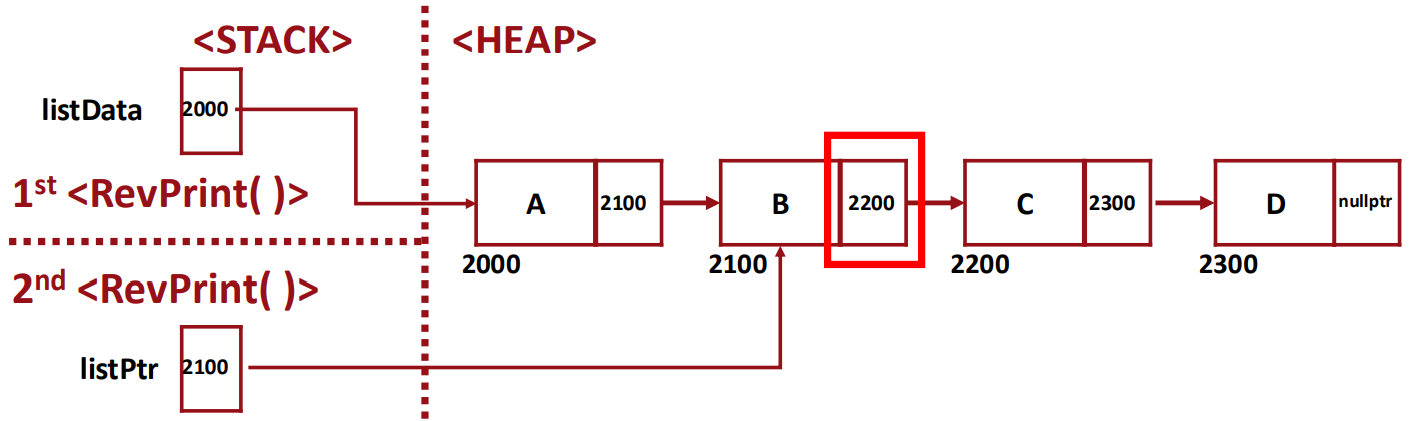

▶ From Memory Map Perspective: call-by-value Parameters

▶ From Memory Map Perspective: call-by-value Parameters
- 가정: 세 번째 recursion 내부에서 listPtr = listPtr->next
- copy된 값에 변화를 만드는 것이기에, 실제로 original 값에는 변화를 만들지 X

▶ When RevPrint(listPtr) is called:
- Since listPtr != nullptr, it will call RevPrint(listPtr -> next).
- It passes the pointer "listPtr -> next" through a call-by-ref.
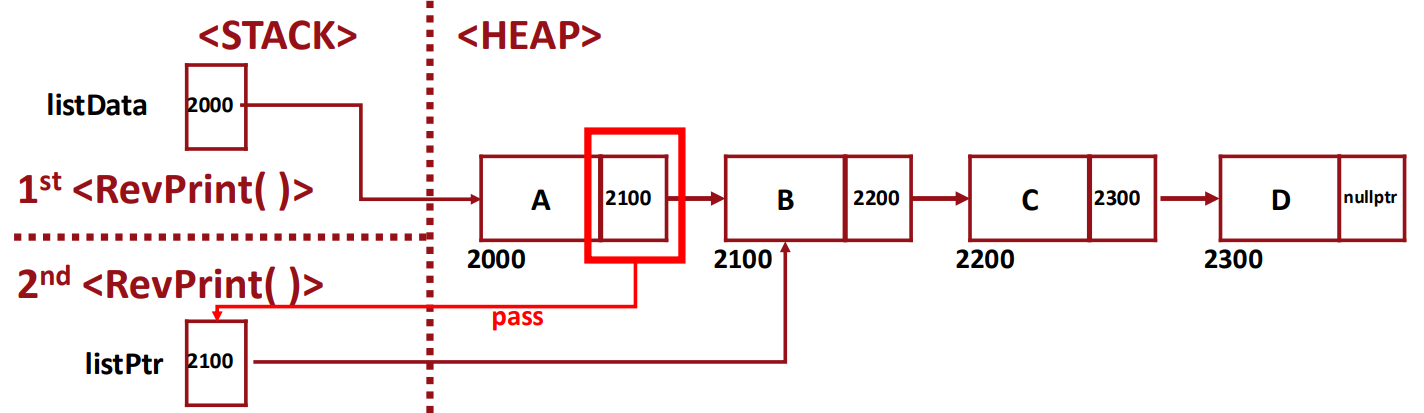
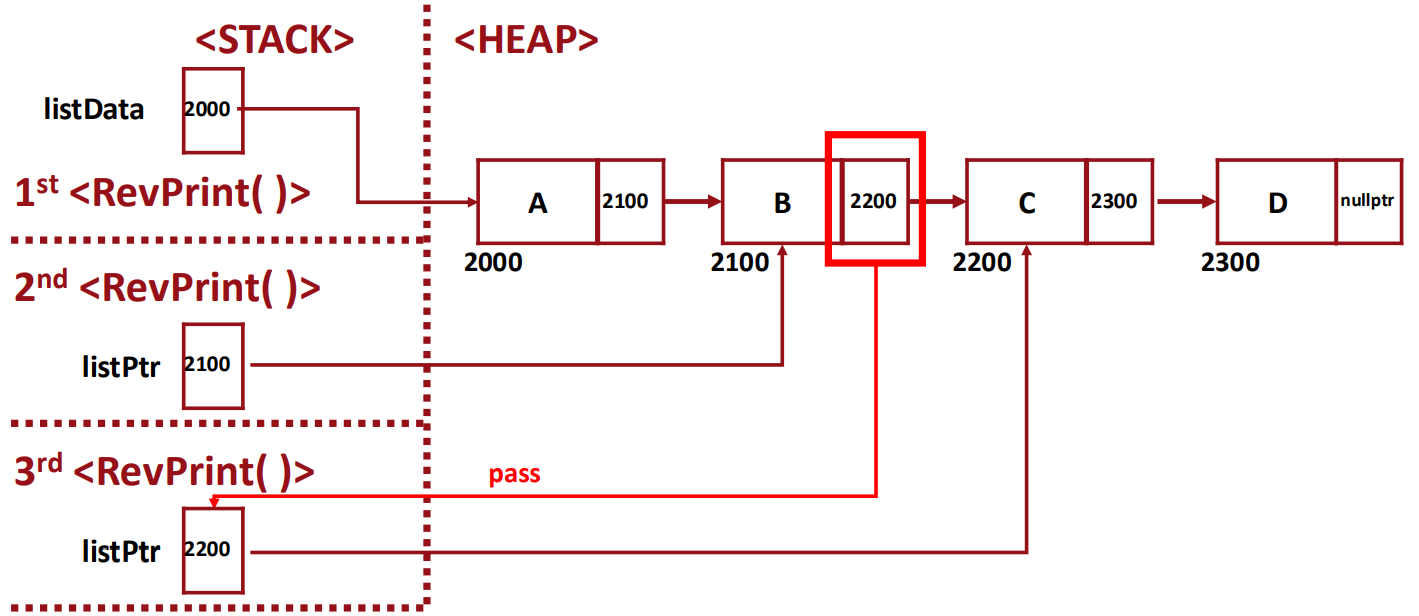
▶ From Memory Map Perspective: call-by-reference Parameters
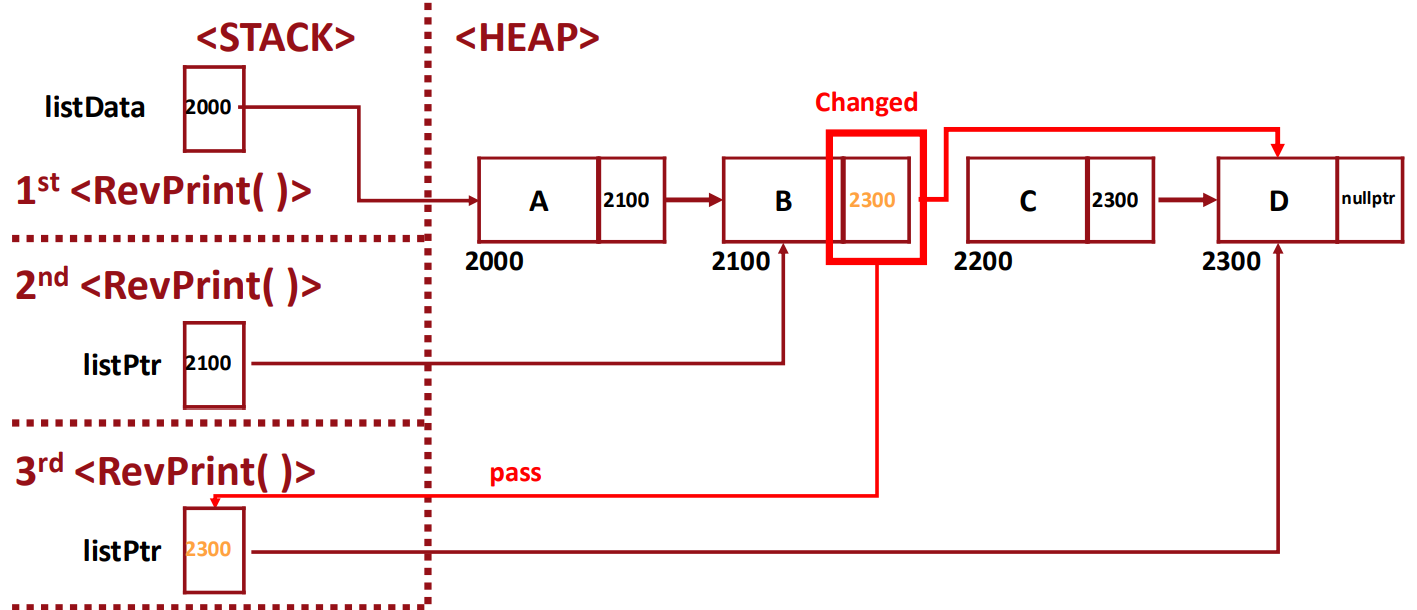
▶ From Memory Map Perspective: call-by-value Parameters
- 가정: 세 번째 recursion 내부에서 listPtr = listPtr->next
- share the same memory space -> original 값에도 변화 O
Understanding Pass-by-reference
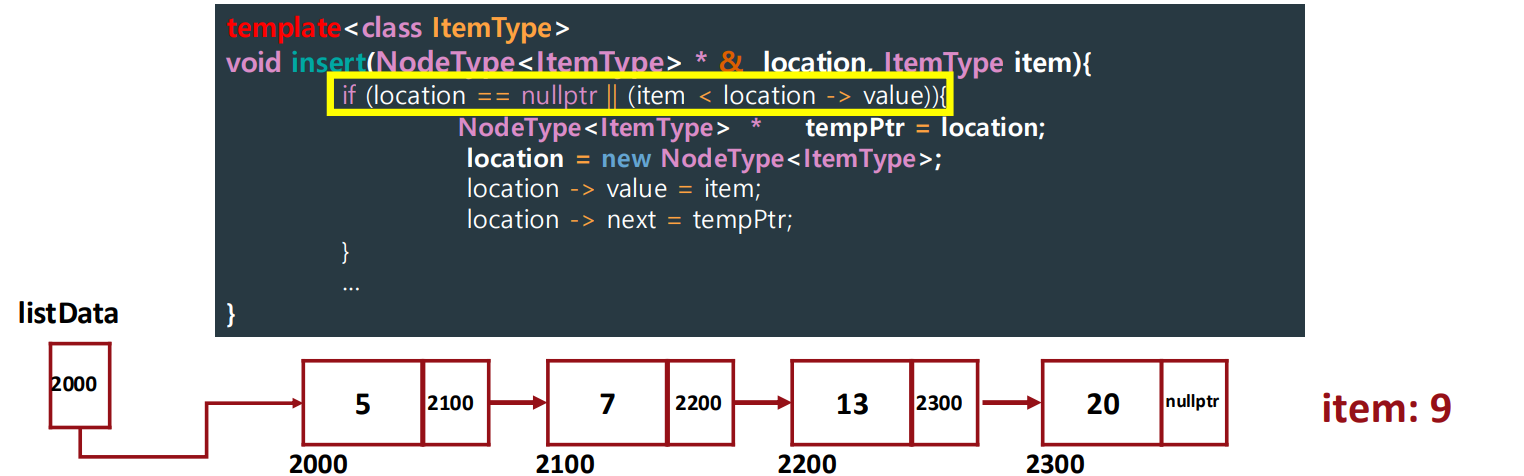
▶ Call-by-reference
How many recursive calls should be called until finding the proper location?
- 3 times (listData, listData -> next, listData -> next -> next)
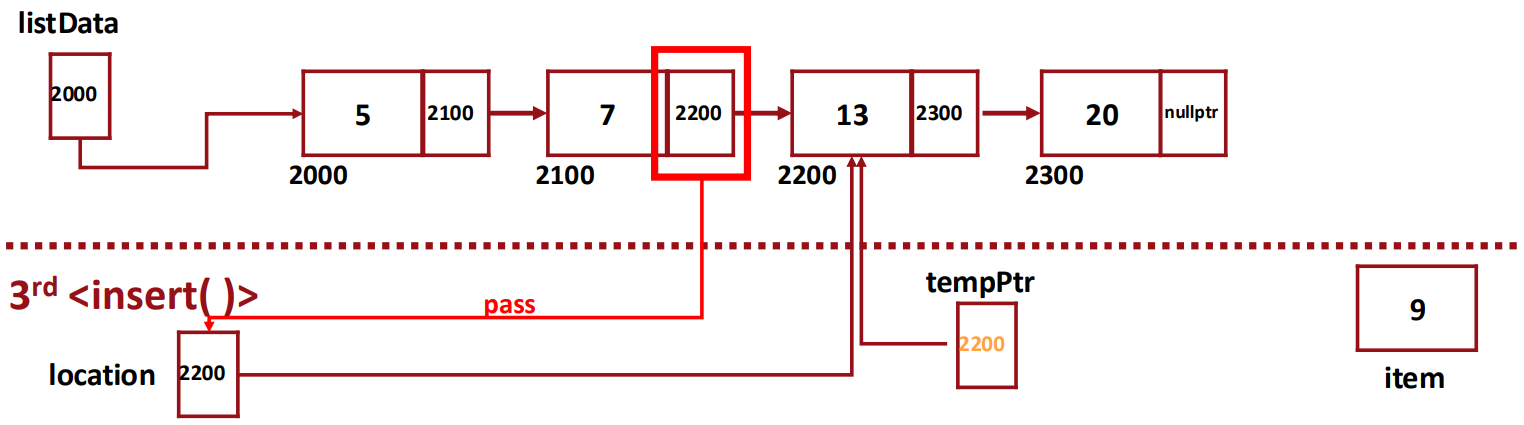
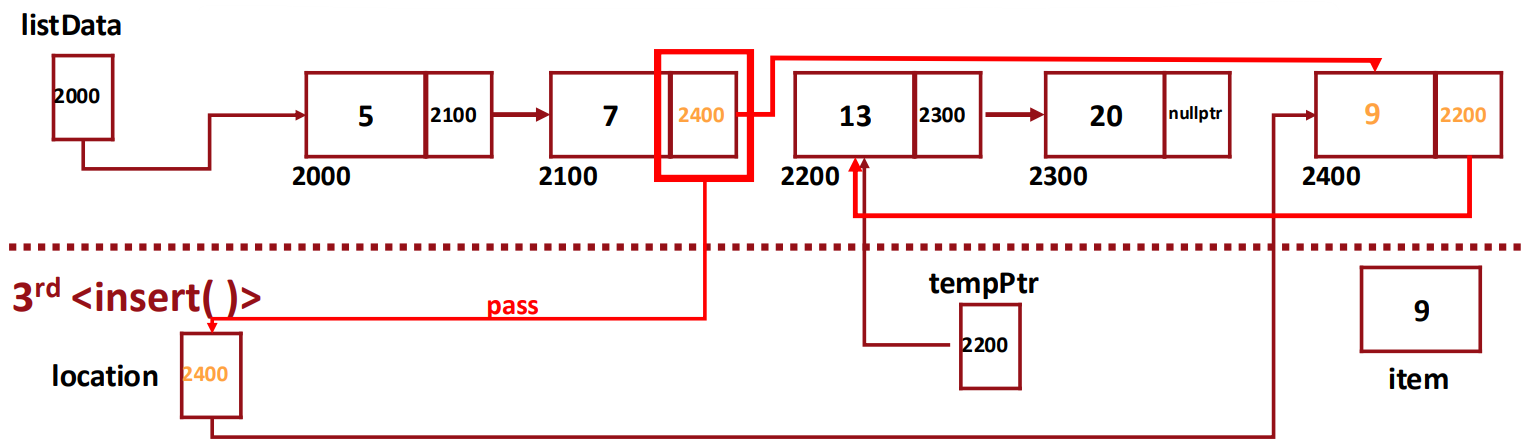

▶ memory map
By generating a new node using "location (call-by-reference parameter)", we do not have to update two pointers.
- call-by-ref -> new 하는 과정에서 pointer 하나가 update되기 때문
deleteItem()


▶ deleteItem() using Recursion
How many recursive calls should be called until finding the proper node?
- 3 times (listData, listData -> next, listData -> next -> next)




▶ memory map
Tail Recursion
last statement, 즉 마지막 instruction 부분이 recursion을 갖는 recursion을 말한다.
때문에 주로, return과 같이 recursion이 일어나게 된다.
▶ Iterative Solution

▶ Recursive Solution
함수가 호출되면 process memory map 중에 stack이라는 segment 안에 activation record가 생긴다.
- activation record: 함수에 대한 local variable, return address 등을 담음
즉, recursion이 한 번 일어날 때마다 stack segment 안에 똑같은 함수에 대한 새로운 activation record들이 쌓인다.
때문에, 일반적으로 iterative solution에 비해서 recursive solution이 stack overflow가 발생할 위험이 훨씬 크다.
이렇게, 시간 복잡도 뿐만 아니라 메모리 사용량 측면에서도 recursion이 더 비효율적인 경우가 많다.
하지만 컴파일러에서는 tail recursion의 경우 알아서 최적화를 해준다.
굳이 필요 없는 정보까지 담긴 activation record를 유지하지 않고, return address와 같이 꼭 필요한 정보만 남기고 activation record 자체를 소멸시켜 버림으로써 recursion이 반복적으로 일어나도 stack overflow가 발생하지 않도록 한다.

▶ RevPrint()
- 마지막 부분에서 recursion이 발생하는 것이 아니기에 tail recursion X -> activation record 만들어짐 (최적화 X)
- 마지막 부분에서는 print를 하고 있음 (argument or local variable 필요)
정리하자면, tail recursion은 함수에서 recursion이 하나 뿐이고, 그 recursion이 함수의 마지막 명령어인 것을 말한다.
Inefficient Recursion (memoization)

- Time Complexity: O(2^N)
- 중간값을 메모리에 저장함으로써 중복되는 연산을 제거하면 O(N)도 가능
- combination 뿐만 아니라, 피보나치도 가능
'CS > 자료구조' 카테고리의 다른 글
| Chapter 8: Tree (2) | 2025.06.08 |
|---|---|
| Programming Exercise: Lab #6 (3) | 2025.06.02 |
| Programming Exercise: Lab #5 (0) | 2025.05.20 |
| Chapter 6: Linked Structures (2) (5) | 2025.05.20 |
| Programming Exercise: Lab #4 (1) | 2025.04.19 |