경희대학교 김정욱 교수님의 컴퓨터 구조 수업을 기반으로 정리한 글입니다.
Floating Point

▶ C code example
위 코드를 보면 "Hello World!"가 10번 반복될 것 같지만,
실제로는 무한히 반복한다.
그렇다면, 컴퓨터 속 2진수를 사용해 floating point를 어떻게 나타내야 할까?
Floating point (부동 소수점)
Floating Point는 쉽게 말해, 소수점이다.
Floating point는 분수, 엄청 큰 수 (ex) 10^20), 엄청 작은 수 (ex) 10^-20)를 나타낼 때 사용된다. (실수 표현 방식)
때문에 값을 나타내는 가수부와 소수점의 위치를 나타내는 지수부로 이루어진다.
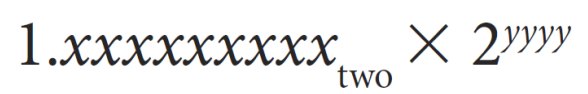
▶ Normalized scientific notation (Binary)
ex) 0.101 -> 1.01 × 2^-1
장점
- 모든 숫자 표현 가능
- 일관성 유지 (지수는 지수끼리, 가수는 가수끼리)
- 소수점 표현을 더 많이 할 수 있어 정확도가 높음
Floating Point Representation (Single Precision)
Single Precision
32-bit만 가지고 표현하는 것을 의미한다.

▶ Single Precision
- Sign (1 bit): 부호 (0 -> 양수, 1 -> 음수)
- Fraction (23 bits): 소수점 단위, 0 또는 1로 소수 23번째 자리까지 표현 가 ex) 1.xxx에서 xxx 부분을 말한다.
- Exponent (8 bits): 2의 지수승
※ 이때, 32비트만 주어지면 Floating Point라는 걸 알 수 없다. instruction으로 정체성을 부여해 주어야 한다.
Floating Point Representation (Problem)
Single Precision Problems
1. Overflow (floating pint)
111111(exponent 8bits), 즉 2의 255승 보다 더 큰 값을 표현하고자 할 때 발생한다.
2. Underflow (floating point)
2의 마이너스 승을 더 작은 값을 표현하고자 할 때 발생한다.
Single Precision은 표현할 수 있는 값의 범위가 2의 지수승이 8bits로 고정되어 있기에 위와 같은 문제가 자주 발생한다.
Floating Point Representation (Solution)
Double Precision

▶ Single precision: 32 bits / Double precision: 64 bits
- exponent 8 bits -> 11 bits: 더 큰 수 표현 가능
- fraction 23 bits -> 52 bits: 더 깊은 소수점까지 표현 가능
Double precision은 32 bits가 아닌, 64 bits로 값을 표현하기에, 더 정확한 값을 표현 가능하다.
하지만 그만큼 Single precision이 속도가 더 빠르다.
Floating Point Representation (IEEE 754)
IEEE 754
floating point를 표현하는 가장 널리 쓰이는 표준어이다.

▶ IEEE 754
- Single precision: 실제론 24 bits 표현 가능 (1 + 23 bits)
- Double precision: 실제론 53 bits 표현 가능 (1 + 52 bits)
※ 1.xxxx일 때 각 x들이 s1, s2, s3, s4를 나타낸다. 때문에 s1이 1이면 0.5, s2가 1이면 0.25 이런 식으로 값을 의미한다.
1. Single precision (IEEE 754)
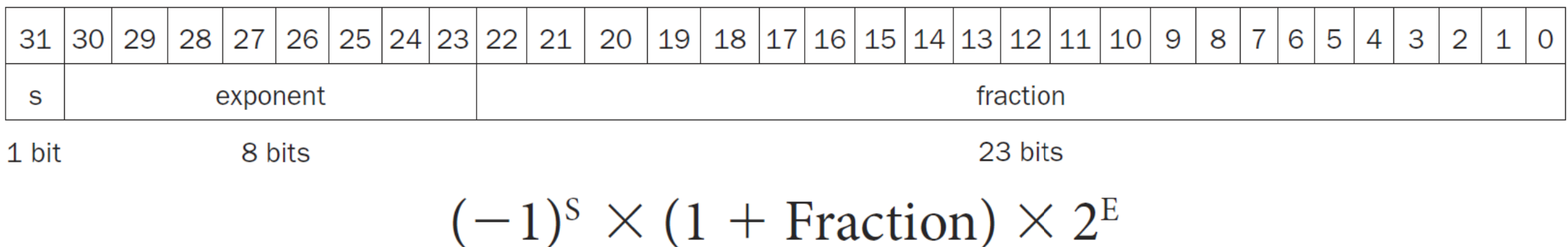
▶ Single precision

▶ Single precision Example
- 양수
- xx = 0
- yy = 1
2. Double precision (IEEE 754)

▶ Double precision
Problem
Problem 1 - Comparision two values

▶ Problem 1 - Comparision two values
마이너스 승도 표기할 수 있어야 한다.
때문에 exponent의 값의 MSB가 0이면 양수, 1이면 음수로 판단해야 한다.
하지 만 값만 봤을 땐 MSB가 1인 게 커보이며, MSB가 무엇이냐에 따라 상황을 나눠 비교하는 게 어렵다.
쉽게 말해, 위 사진에서 위의 값이 아래의 값보다 크다는 것을 직관적으로 이해하기 어렵다.
Problem 2 - Hard to handle the exceptional cases
지수가 무한대 혹은 마이너스 무한대일 경우와, NaN 같은 예외처리를 할 수 없다.
Solution - Biased notation

▶ Based notation
ex) exponent가 00000001 -> 1 - 127하여 2^-127 / exponent가 11111110 -> 254 - 127하여 2^127
Bias value 127 (Single precision)
Range - The smallest value

▶ The smallest value
※ 이때, 0은 예외처리(floating 값 X)를 위에 남겨두기에 1부터 시작한다고 이해하면 된다.
Range - The largest value

▶ The largest value
※ 이때, 전부 1인 것(floating 값 X)은 예외처리를 위에 남겨둔다.
Bias value 1023 (Double precision)
Range - The smallest value

▶ The smallest value
Range - The largest value
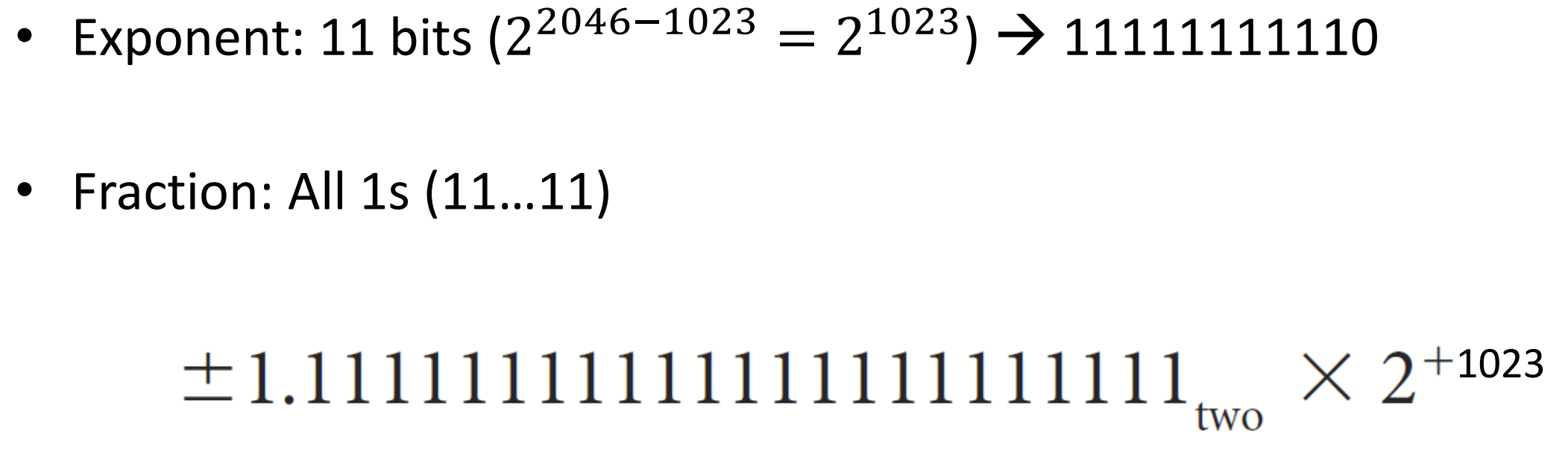
▶ The largest value
지수승이 다 0일 때와 1일 때 무슨 일이 발생할까?
Exponent 00...00과 11...11은 저장되어 있다.
Zero
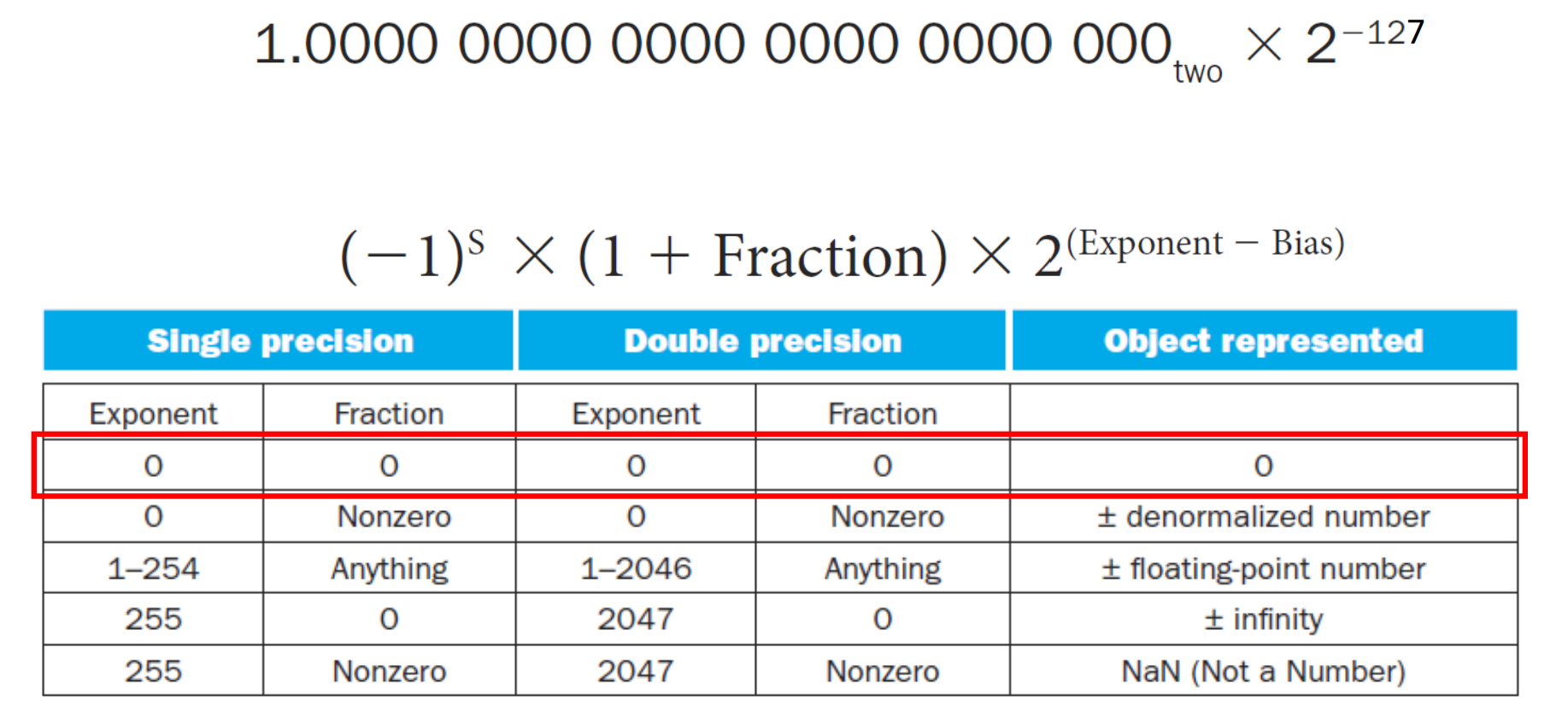
▶ Exponent 00...00 and Fraction 0 -> zero
만약 0으로 인식한다는 예외처리를 주지 않으면 1.0000.. × 2^-127로 약간의 차이가 발생한다.
물론 1.0000.. × 2^-127도 매우 작은 값으로 0과 가깝지만 0은 아니기에 예외처리를 해주는 것이다.
Denormalized number
표현할 수 있는 범위보다 작은 수를 표현할 때 사용한다.

▶ Exponent 00...00 and Fraction Nonzero -> 표현할 수 있는 범위보다 작은 수 표현
single precison의 경우, 1.0 × 2^-126이 가장 작은 수인데, 이보다 더 작은 수를 표현하고 싶을 때 사용한다.
이를 사용하면 소수점을 더욱 정확하게 표현할 수 있다.
지수승은 2^-126(1-127)로 고정한 상태에서 (1 + Fraction)에서 1을 무시하고 Fraction만 사용한다.
때문에 표현할 수 있는 가장 작은 수는 0.0000...1 × 2^-126, 즉 1.0 × 2^-149이다.
Infinite / NaN

▶ Exponent 11...11 and Fraction 0 -> Infinite / Exponent 11...11 and Fraction Nonzero -> NaN(Not a number)
※ NaN ex) 0/0
Floating Point Representation (Example)
Example 1

▶ 10진수 -> 2진수
0.75 × 2 = 1 + 0.5
0.5 × 2 = 1
-> 0.11 (2진수)

▶ 2진수 -> normalized scientific notation (1.xx × 2^yy)

▶ single precision

▶ double precision
Example 2

▶ Converting binary to decimal floating point
0.01
-> 0 × 2^0 + 0 × 2^-1 + 1 × 2^-2 = 0.25 (10진수)
Floating Point Addition
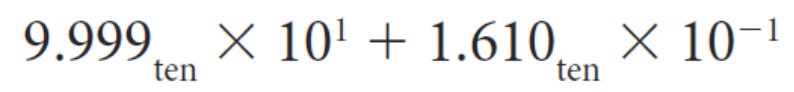
▶ Example
Step 1. 가장 큰 지수승으로 통일한다.

▶ Step 1
※ Suppose only four decimal digits -> 문제 가정에 의해 소수점 4번째부터 버린다. (반올림)
Step 2. 더한다.
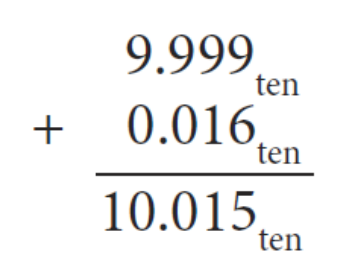
▶ Step 2
Step 3. Normalize the sum, 이때 Overflow 혹은 Underflow 발생하였는지 확인한다.

▶ Step 3
이때 지수승인 2이므로 -126 < 2 < 127 이기에 Overflow 혹은 Underflow가 발생하지 않음을 확인할 수 있다.
Step 4. Round the sum

▶ Step 4
문제 가정에 의해 소수점 4번째부터 버리기로 하였으니 반올림하여야 한다.
Floating Point Addition (Example)
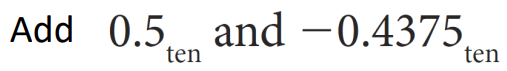
▶ Example
Step 0. 10진수 -> 2진수 -> Normalized scientific notation
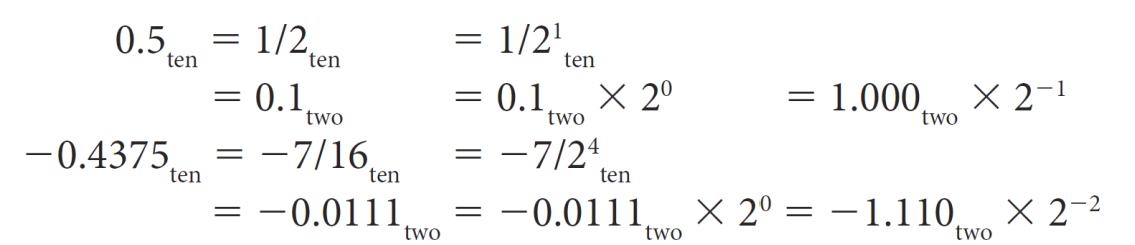
▶ Step 0
0.5 × 2 = 1
-> 0.1 (2진수)
0.4375 × 2 = 0 + 0.875
0.875 × 2 = 1 + 0.75
0.75 × 2 = 1 + 0.5
0.5 × 2 = 1
-> 0.0111 (2진수)
Step 1. 가장 큰 지수승으로 통일한다.

▶ Step 1
※ Suppose only four decimal digits -> 문제 가정에 의해 소수점 4번째부터 버린다. (반올림)
Step 2. 더한다.

▶ Step 2
Step 3. Normalize the sum, 이때 Overflow 혹은 Underflow 발생하였는지 확인한다.

▶ Step 3
Step 4. Round the sum

▶ Step 4
Step 5. 2진수 -> 10진수

▶ Step 5
0.0001
-> 0 × 2^0 + 0 × 2^-1 + 0 × 2^-2 + 0 × 2^-3 + 1 × 2^-4 = 2^-4 = 1/16 = 0.0625(10진수)
Floating Point Multiplication

▶ Example
Step 1. Calculate the exponent of the product

▶ Step 1
곱셈은 지수는 지수끼리 fraction은 fraction끼리 따로 계산한다.
-> 5 + 127 = 13.
Step 2. Multiply the significands

▶ Step 2
Step 3. Noralize the value if the product is unnormalized

▶ Step 3
Step 4. Round the number

▶ Step 4
Step 5. Determine the sign
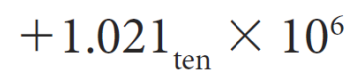
▶ Step 5
Floating Point Multiplication (Example)

▶ Example
Step 0. 10진수 -> 2진수 -> Normalized scientific notation

▶ Step 0
Step 1. Calculate the exponent of the product

▶ Step 1
-3 = 124 - 127
Step 2 & 3. Multiply the significands & Noralize the value if the product is unnormalized
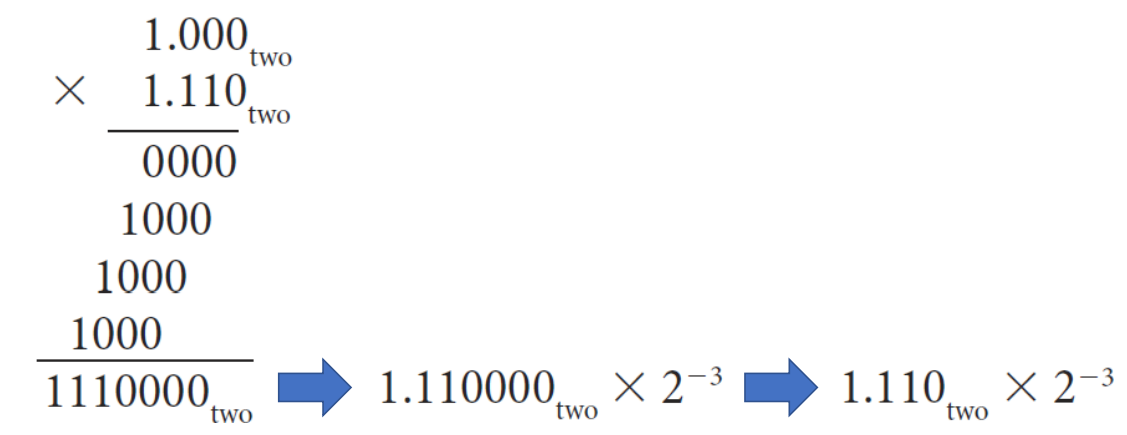
▶ Step 2 & 3
Step 4. Round the number

▶ Step 4
Step 5. Determine the sign

▶ Step 5
(+) × (-) = (-)
Step 6. 2진수 -> 10진수

▶ Step 6
'CS > 컴퓨터구조' 카테고리의 다른 글
| Lecture 13: The Processor - 2 (0) | 2024.11.29 |
|---|---|
| Lecture 12: The Processor - 1 (1) | 2024.11.27 |
| Lecture 09: Arithmetic for Computers - 1 (1) | 2024.10.16 |
| Lecture 08: Instructions - Language of the Computer - 5 (5) | 2024.10.14 |
| Lecture 07: Instructions - Language of the Computer - 4 (1) | 2024.10.14 |