경희대학교 김정욱 교수님의 컴퓨터 구조 수업을 기반으로 정리한 글입니다.
Arithmetic Operation

▶ MIPS code

▶ ALU (Arithmetic and Logical Unit)
ALU
사칙 연산을 담당하는 하드웨어이다. (덧셈, 뺄셈, 곱셈 - 덧셈의 연속, 나눗셈 - 뺄셈의 연속)
- 입력 2개: 연산할 레지스터 2개에 대응하는 각각의 값들
- Opcode: 어떤 연산을 할지 결정
- 출력 2개: 연산 결과를 저장할 레지스터, Overflow 확인 위한 Status
Addition and Subtraction
1. Addition (binary)

▶ Addition

▶ carry (올림수)
carry: 올림수
2. Subtraction (binary)

▶ Subtraction: A - B (뺄셈)

▶ Subtraction: A + (-B) (보수의 덧셈)
보수: 0 <-> 1 뒤집은 후 + 1
Overflow
Overflow는 표현할 수 있는 범위를 벗어난 것을 의미하며,
MSB가 바뀐 것(0 <-> 1)으로 Overflow가 일어났음을 알 수 있다.
또한, 부호가 바뀌는 개념이기에 sign bit의 경우에만 생각한다.
※ MSB가 0이면 양수, 1이면 음수이다.
1. Addition
더하기의 경우에는 두 수의 부호가 갔을 때 Overflow가 발생할 수 있다.
연산하는 두 수의 부호가 다른 경우에는 두 수가 상쇄되기에 표현할 수 있는 범위 내에 존재하게 되어 Oveflow가 발생할 수 없다.
※ 이때, 발생할 수도 있다는 것이지, 무조건 발생한다는 의미가 아니다.

▶ Addition Overflow
- 양 + 양 = 음
- 음 + 음 = 양
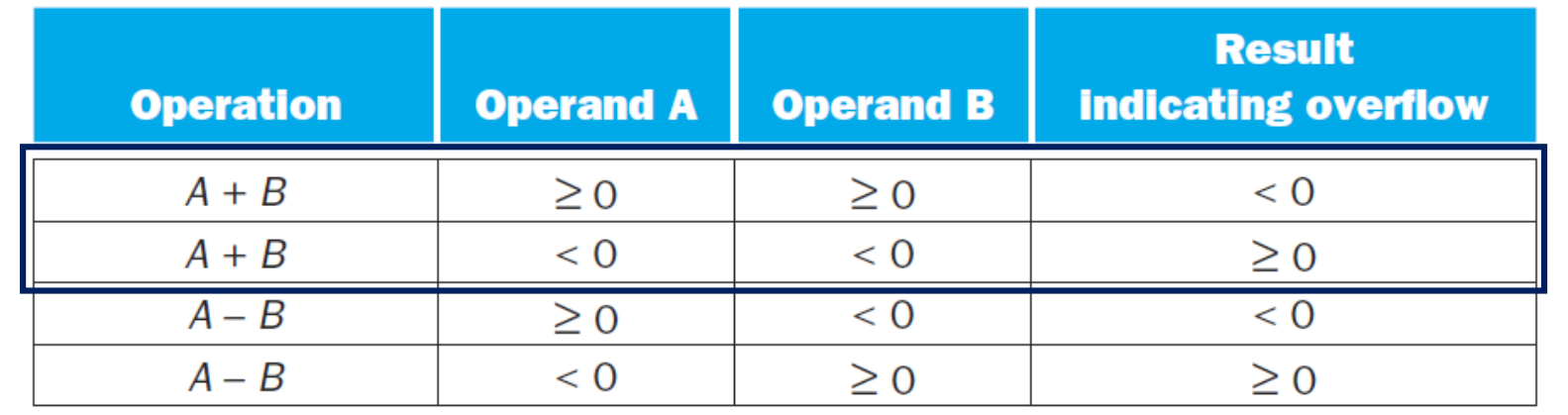
▶ Addition Overflow
2. Subtraction
빼기의 경우에는 두 수의 부호가 다를 때 Overflow가 발생할 수 있다. (부호 반대일 )

▶ Sbutraction Overflow
- 양 - 음 = 음
- 음 - 양 = 양
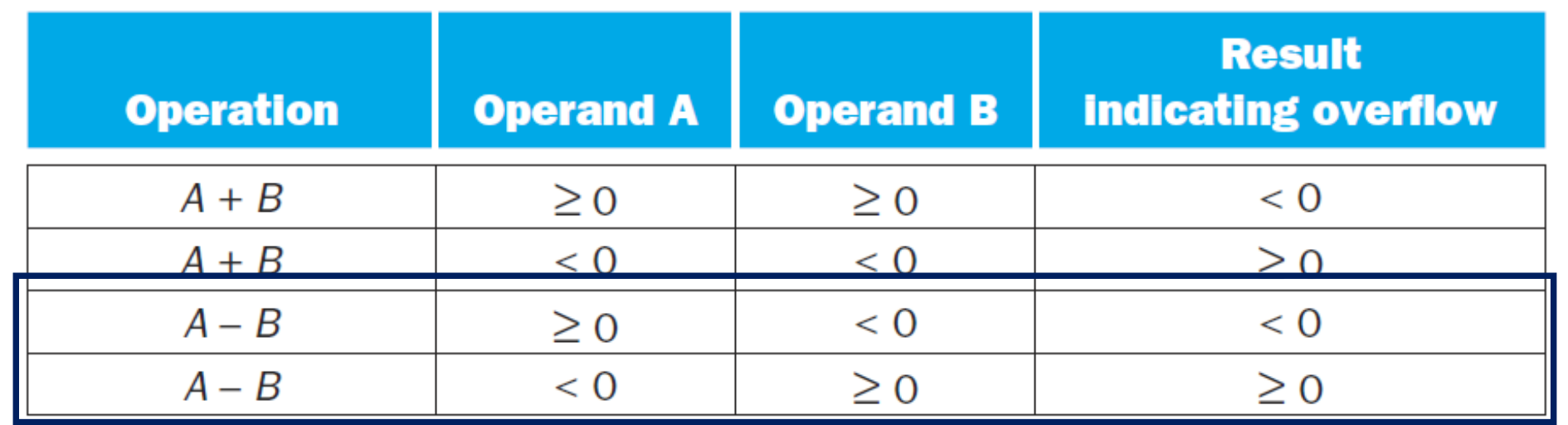
▶ Sbutraction Overflow
32 bits 자체를 보고, 즉 단순히 비트만 봐서는 sign인지, unsign(무조건 양수, 부호 X)인지 알 수 없다.
때문에, instrucion을 통해 32 비트를 sign으로 볼지, unsign으로 볼지 결정이 가능하다.
Signed instructions
- Add (add)
- Add immediate (addi)
- Subtract (sub)
Unsigned instructions
- Add unsigned (addu)
- Add immediate unsigned (addiu)
- Subtract unsigned (subu)
※ sign일 때는 MSB가 1이면 음수, 0이면 양수, 즉 MSB가 부호를 판단하는 기준이 된다. 하지만 unsign일 경우에는 MSB가 1이더라도 단순히 큰 값으로만 인식한다.
※ carry 발생으로 MSB에 있던 값이 밀려 무시되는 것은 overflow가 아니다.
⭐ Overflow (MIPS C Assembly Code

▶ Overflow 확인
- 두 수의 부호가 같은지 확인 (Overflow 발생 가능성 확인), 부호가 같으면 파란색으로 이동 - MSB XOR
- Overflow 발생 여부 확인 - 연산 결과의 MSB와 연산 전 값의 MSB XOR
XOR: 대응되는 두 비트가 서로 같으면 0, 다르면 1
slt $t3, $t3, $zero▶ $t3의 값이 0 보다 작은지, 즉 $t3의 값이 음수인지를 확인하는 코드 (sign instruction slt-> $t3의 값의 MSB가 1이면 음수)
xor $t3, $t0, $t1▶ Overflow가 발생하지 않았으면, 즉 MSB가 바뀌지 않았으면 $t0와 $t1의 MSB 값이 같아 $t3의 MSB 값은 0이 됨 (양수)
⭐ 더하기는 두 수의 부호 같을 때, 빼기는 두 수의 부호 다를 때 overflow 가능성이 있다.
Multiplication

▶ Multiplication
- Multiplicand: 곱함을 당하는 수
- Multiplier: 곱하는 수
Multiplication - Atithmetic and Logical Unit (ALU)
Multiplication
- When bit in multiplier: place a copy of the multiplicand in the proper place
- When bit 0 in multiplier: place 0 in the proper place
-> 곱셈: 덧셈의 반복

▶ ALU (Arithmetic and Logical Unit)
1. 출발점: product = 0 (초기화)
2. Multiplier의 각 비트를 하나씩 확인하며 진행되는데, 먼저 Multiplier의 LSB부터 1인지 확인하는 Control test를 거친다. 이때 1이면 Multiplicand를 복사해 적당한 위치에 값을 넣어 Product에 누적하고, 0이면 그냥 넘어간다. 그리고 다음 비트로 갈 때에는 Multiplicand는 sll을 하여 적당한 위치를 찾고(자릿수), Multiplier은 srl을 하여 다음 비트 확인을 위해 LSB를 버리도록 한다. 즉, 이런 식으로 Product Update를 한다.
3. 32비트는 이렇게 32번 반복하며, Product는 누적된 최종 결과값이다.

▶ Multiplication algorithm in ALU
32-bit가 아닌 64-bit ALU를 사용하는 이유가 뭘까?
multiplicand를 sll 할 때, 즉 값을 왼쪽으로 옮길 때 값의 손실을 막기 위해 64-bit를 사용한다. (32-bit 2개)

▶ Example - Multiply 2 and 3 (1)
※ 10진수는 2진수로 바꾸면 무조건 32bit이다. 즉, 위에선 0을 편의를 위해 생략한 것 뿐이지, 실제론 32bit이다.

▶ Example - Multiply 2 and 3 (2)
Division

▶ Division
- Dividend: 나누어지는
- Divisior: 나누는 수
- Quotient: 몫
- Remainder: 나머지
-> Dividend = Quotient × Divisor + Remainder
Division - Arithmetic and Logical Unit (ALU)
Division
- When dividend is larger than divisor: Quotient is 1 and subtract
- When dividend is smaller than divisor: Quotient is 0 and place below 0
-> 나눗셈: 뺄셈의 반복
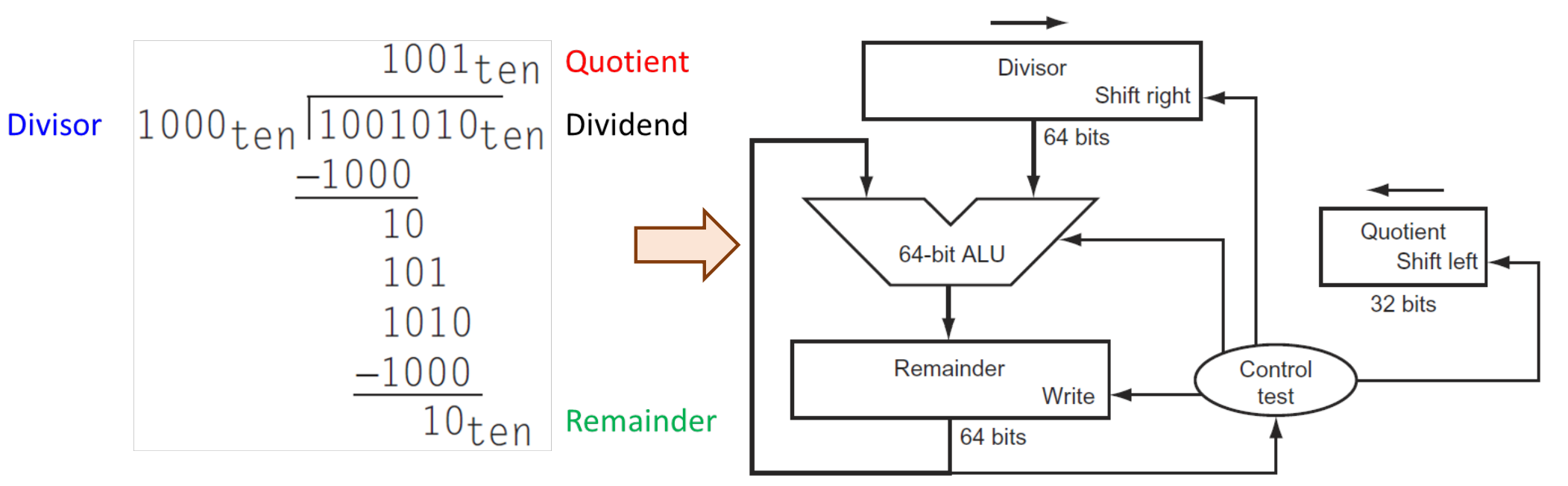
▶ ALU (Arithmetic and Logical Unit)
1. 초기 Remainder를 Dividend로 초기화 한다.
2. Divisor 값이 Remainder보다 큰지, 작은지 확인하는 Control test를 해준다. 이에 따라 Quotient를 1 혹은 0으로 해준 후 Quotient는 sll, Divisor은 srl을 하며 Divisor를 빼주는 과정을 반복한다. 이때, Remainder - Divisor를 했을 때 MSB가 0에서 1로 바뀌었다는 것으로부터 Remainder 보다 Divisior이 더 크다고 판단할 수 있다.
ex) 46 나누기 5: 46 − 5 × 2^3 − 5 × 2^0 = 1
32-bit가 아닌 64-bit ALU를 사용하는 이유가 뭘까?
32bit를 핸들링 한다는 것은 32bit Dividend에서 계속 Divisor 값을 오른쪽으로 이동해가며 빼야 하는데, 이런 식으로 Divisor을 오른쪽으로 이동시키려면 Dividend 쪽에서 앞 32비트를 0으로 채우고, Divisor는 뒤 32비트를 0으로 채워 비트 연산을 수행해야 하기 때문이다.
이렇게 32비트 연산을 할 때에는 32번이 아니라, 총 33(32 + 1)번의 빼기의 반복이 있어야 한다.

▶ Division algorithm in ALU (Example - Dividing 7 by 2 (1))

▶ Example - Dividing 7 by 2 (2)
나누기가 느린 이유가 뭘까?
나누기는 뺀 다음 검증 후, 빼면 안 된다고 판단되면 다시 돌아오는 과정이 여러번 반복된다.
즉, 검증 후 다시 돌아오는 과정 때문에 나누기가 느린 것이다.
※ 처리 속도: 덧셈 = 뺄셈 > 곱셈 > 나눗셈
Summary

▶ MIPS assembly language
※ mult, multu, div, divu만 기억하면 된다.
'CS > 컴퓨터구조' 카테고리의 다른 글
| Lecture 12: The Processor - 1 (1) | 2024.11.27 |
|---|---|
| Lecture 10: Arithmetic for Computers - 2 (0) | 2024.10.17 |
| Lecture 08: Instructions - Language of the Computer - 5 (5) | 2024.10.14 |
| Lecture 07: Instructions - Language of the Computer - 4 (1) | 2024.10.14 |
| Lecture 06: Instructions - Language of the Computer - 3 (10) | 2024.10.08 |