경희대학교 김정욱 교수님의 컴퓨터 구조 수업을 기반으로 정리한 글입니다.
ROM vs. RAM
ROM (Read Only Memory)
- Write는 못하고 (저장 불가) Read만 할 있는 Memory
- Non-volatile memory (비휘발성 메모리): 전원이 꺼져도 데이터가 없어지지 않음
※ Mask ROM: 반도체 생산 공정인 마스킹 단계에서 고정된 데이터 회로 패턴으로 생산하는 방식 (책을 대량 인쇄하는 것처럼)
※ ROM은 공장에서 애초에 0과 1의 패턴들이 다 만들어져 나오기에 Write 할 수 없다.

▶ ROM
RAM (Random Access Memory)
- temporary Memory
- Read-write memory: 읽고, 쓰기 둘 다 가능
- Volatile memory (휘발성 메모리): 컴퓨터가 작동 중 (ON)일 때 임시적으로 데이터 저장
※ RAM ex) DRAM, SRAM

▶ RAM
SRAM vs. DRAM
SRAM (Static Random Access Memory)
- chche momory
- 한 비트를 표현하기 위해 최소 6개 이상의 트랜지스터 필요: DRAM에 비해 집적도가 낮고 소비 전력이 큼
- 플립플롭 소자로 구성: 전원이 연결되어 있는 동안에는 내용을 계속 유지
- 속도가 빠르다: SRAM은 capacitor를 사용하지 않아 refresh (충전)이 필요 없음
※ 트랜지스터: 0 or 1 값을 가진다.
※ 집적도가 낮다는 것은 한 비트를 표현하는 데에 공간을 많이 차지한다는 의미이다.

▶ SRAM
BL과 BL바는 하나는 set, 다른 하나는 reset으로, 두 입력은 서로 다른 값을 가진다.
set이 1이면 플립플롭에 의해서 1을 유지, reset이 1이면 플립플롭에 의해서 0을 유지한다.
DRAM (Dynamic Random Access Memory)
- 커패시터 사용: 시간이 지나면 스스로 방전됨
- 전원이 계속 공급되더라도 커패시터가 주기적으로 재충전되어야 기억된 내용을 유지할 수 있음
- 회로가 비교적 간단하고 가격이 저렴
- 집적도가 높기 때문에 대용량의 기억 장치에 주로 사용
- 전원이 꺼지면 자료를 계속 보존할 수 없음

▶ DRAM
※ DRAM은 충전이 필요하기에 SRAM 보다 상대적으로 느리다.
SRAM vs. DRAM

▶ SRAM vs. DRAM
Memory Hierarchy
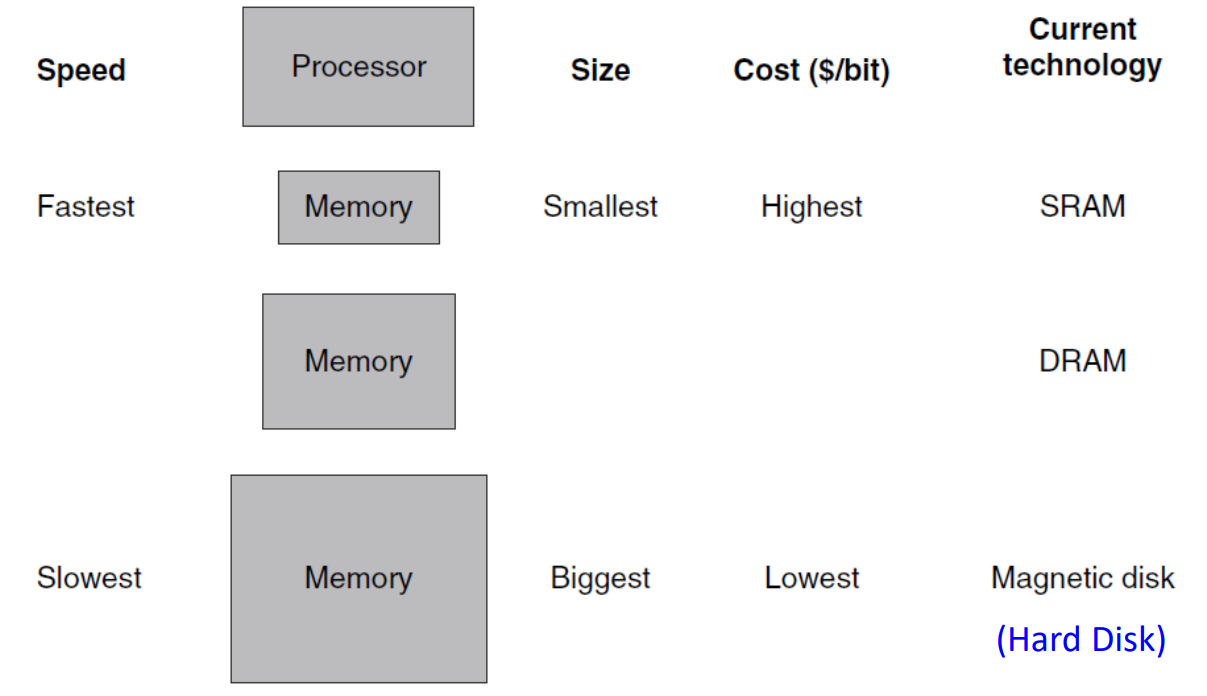
▶ Memory Hierarchy
- SRAM: cache memory
- DRAM: main memory
- Magnetic disk: hard disk
CPU 입장에선 cache (SRAM)랑만 소통한다. 그 이유는 hard disk에 접근하는 속도가 매우 느리기 때문이다.
하드 디스크에는 실제 데이터가 있고, 필요한 값들을 main memory에, 이 순간에 필요한 데이터는 cache에 올린다.
Principle of Locality
Temporal locality
최근에 접근한 item에 대해 나중에 또 접근할 가능성이 높다. (시간적 개념)
Spatial locality
접근된 item에 가까운 주소의 item에 접근할 가능성이 높다. (공간적 개념)
이때, 메모리가 정리 정돈이 잘 되어 있다는 가정이 꼭 있어야 한다.
ex) array
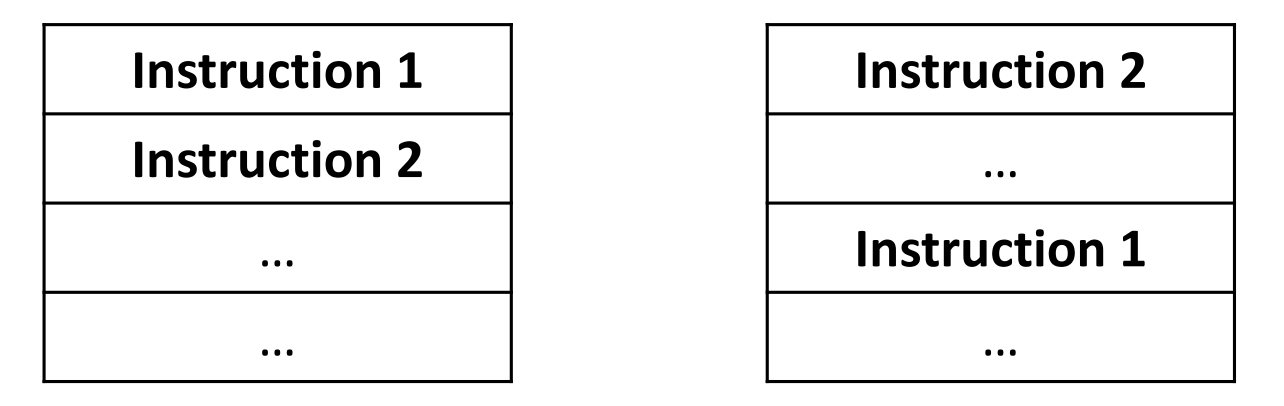
▶ 잘 정리되어 있는 메모리 vs 잘 정리되지 않은 메모리
Block
Copy
main memory 혹은 disk에 있는 원본 데이터를 cache로 가져오는 작업이다.
즉, CPU가 요청한 데이터가 cache에 없으면 필요한 데이터를 가져오기 위해 main memory 혹은 disk로부터 copy를 수행한다.
Block
cache로 데이터를 copy하는 최소 단위이다.
※ Block은 memory의 종류에 따라 copy해 오는 양 (Block의 크기)이 다를 수 있다.

▶ Block: The minimum unit of copying information
If the data appears in the upper level
Hit
upper level (cache)에 데이터가 존재하는 경우를 말한다.
- Hit rate (hit ratio): upper level에 데이터가 얼마나 있는지에 대한 비율이다.
- Hit time: upper level에 데이터가 있는지 확인하고 copy하는 총 시간이다.

PU▶ Hit ratio
If the data not found in the upper level
miss
upper level (cache)에 데이터가 존재하지 않는 경우를 말한다. (<-> miss)
- miss rate (miss ratio): upper level에 데이터가 얼마나 없는지에 대한 비율이다. (miss ratio = 1 - hit ratio)
- miss penalty: lower level에서 upper level로 block을 교체하는 시간 + block을 processor로 전달하는 시간
miss 하더라도, temporal locality 때문에 그 값을 또 부를 확률이 높아 꼭 저장을 해두어야 한다.
※ cache에 데이터가 존재하지 않는 경우는, 한 번도 부른 적이 없거나, 부른 적이 있지만 chche 용량이 작아 지워진 경우이다.
※ CPU 입장에서 데이터를 요청한다는 것은 결과적으로 반드시 존재하는 데이터를 요청한다는 의미이다. 따라서 miss일 경우에도 cache 혹은 main memory 입장에서 없다는 의미이지 맨 밑 disk에는 무조건 저장되어 있다. 즉, miss가 아예 존재하지 않는 데이터를 요청하는 것이 아니다.
Cache Memory
Cache
memory hierarchy 중에서 CPU와 가장 가까운 메모리이다.
이때 CPU는 Cache랑만 소통하기에, CPU 입장에선 다른 메모리가 있는지도 모른다.

▶ Cache Memory Example
- a. Processor (CPU)가 Cache에 Xn 데이터 요청 -> Cache Memory에 없으니 miss
- b. 다른 memory로부터 Xn cache에 copy 하여 가져 옴
Direct-mapped cache
각 memory의 위치가 cache의 정확히 한 위치에 매핑된다.
이때 위치는 modulo 연산을 통해 결정된다.
이 덕에, 요청한 데이터 값을 찾을 때 쉽게 찾을 수 있다는 장점이 있다.

▶ Direct-mapped cache: cache - main memory
※ cache에 8개의 Block (공간) 밖에 없기에 8(1000)로 modulo 연산을 한다.
Cache 안에 데이터 값의 존재 유무는 어떻게 알까?
=> Add a valid bit to a cache
- Valid bit: entry가 valid address (유효한 주소)를 담고 있는지 확인하는 지표 (Indicator)
- Initial valid bit = 0
- cache에 데이터 값이 존재하면 valid bit =1, 존재하지 않으면 valid bit =0
block 한 개당 valid bit가 한 비트씩 필요하다.
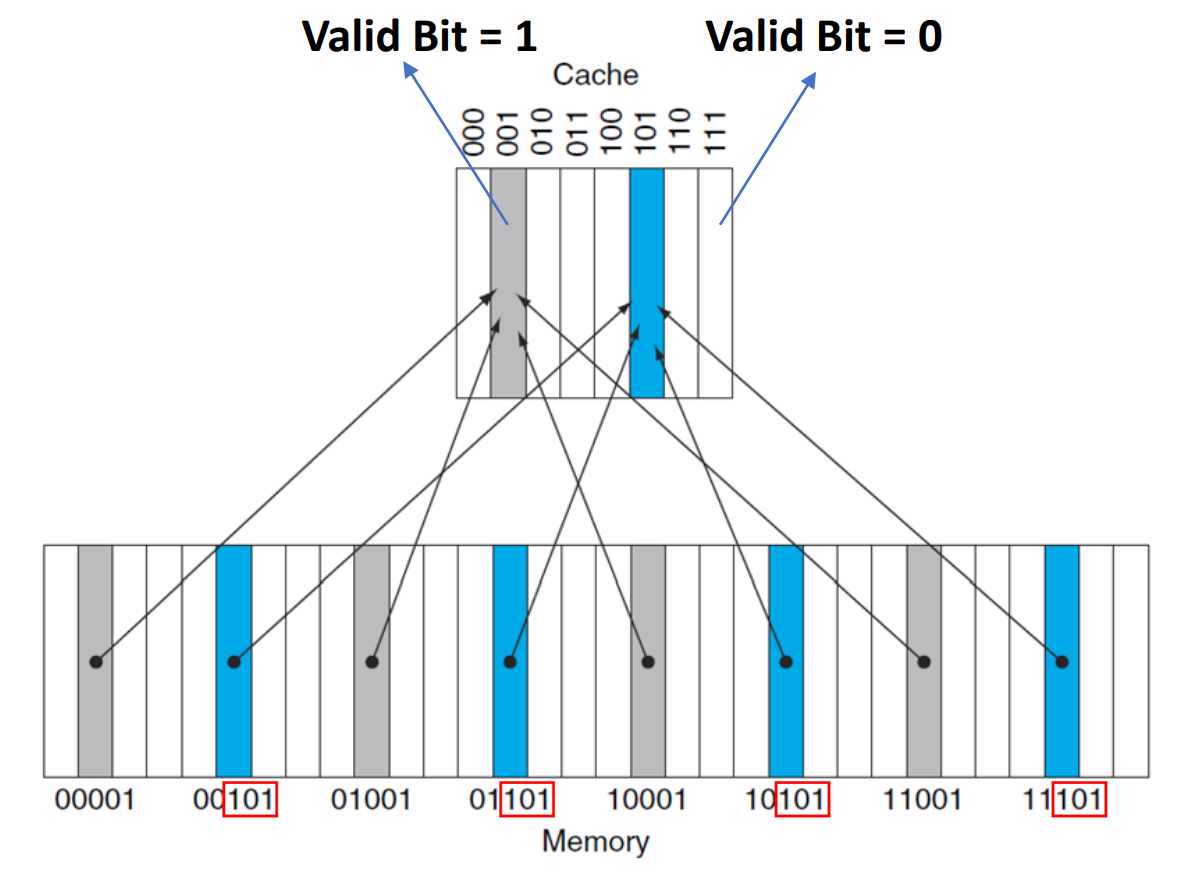
▶ add a valid bit to a cache
Cache 안에 데이터 값이 있을 때, 그 cache 안에 진짜 필요한 값이 있는지는 어떻게 찾아낼까?
ex) 철수인 건 알겠는데, 그게 김철수가 맞는지는 어떻게 확인 할까?
=> Set a tags to a cache를 통해 다 찾아 다닌다
- tag: address information을 포함하여 요청된 word에 적합한 cache의 word를 식별하는 표식
block 한 개당 tag가 여기선 두 비트씩 필요하다.

▶ set a tags to a cache
-> question 2개를 통해 알 수 있는 것은, block 한 개당 여기선 총 세 비트씩 필요하다. 최종적으로 8개의 block로 이루어진 cache에 24개의 추가적인 bit가 필요하다.
Accessing a Cache
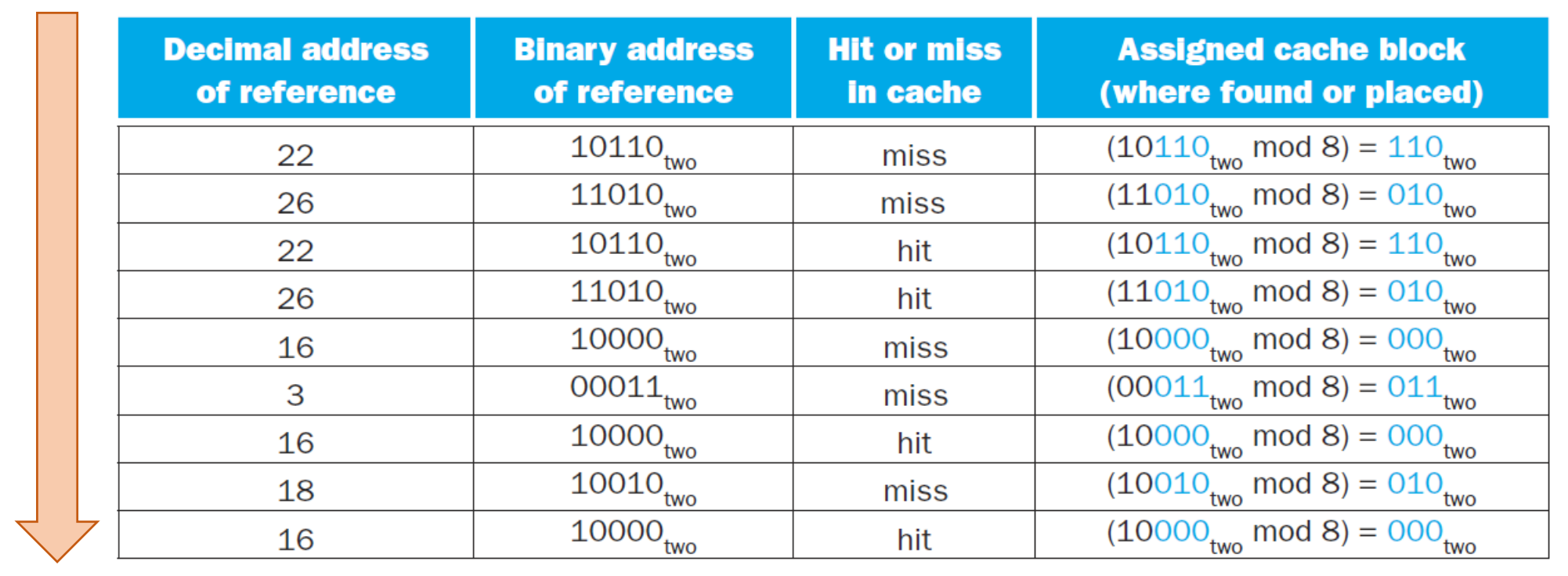
▶ request -> hit or miss -> miss에 대해 cache로 올릴 주소 mapping
※ reference: CPU가 요청한 데이터

▶ Example 1

▶ cache에 copy 1
※ valid bit: 여기선 N/Y으로 나왔지만 실제론 0/1이다.
※ cache엔 block이 8(2^3)개로 cache address는 3개의 bit으로 표현 가능, 이 나머지 비트로 tag 표현하기에 tag 2 bit이다.

▶ Example 2 - cache에 copy 2
22, 26, 16은 처음엔 miss 였지만 miss 때 copy 해 주었기 때문에 또 다시 22, 26, 16이 나올 때 hit 할 수 있는 것이다.
이때 초록색 부분은 데이터가 있긴 하지만 필요한 데이터가 아니기에 기존에 공간을 차지하고 있던 데이터는 버리고 18에서 부른 데로 바꿔준다. 이는 Temporal locality에 의해 가장 최근에 부른 값으로 바뀌는 것이다.
때문에, 정확히 한 곳에만 위치해야 하기에 이렇게 버려진다는 Direct-mapped cache의 점도 있다.
1 word block
하나의 데이터를 가지고 오는 것을 1 word block이라 한다. (하나의 block = 하나의 word)
- Tag field:To compare with the value of the tag field of the cache
- Cache index: To select the block
※ copy 해 오는 최소 단위가 block인데, 이때 최소의 기준이 달라 디테일하게 정의가 필요하다.
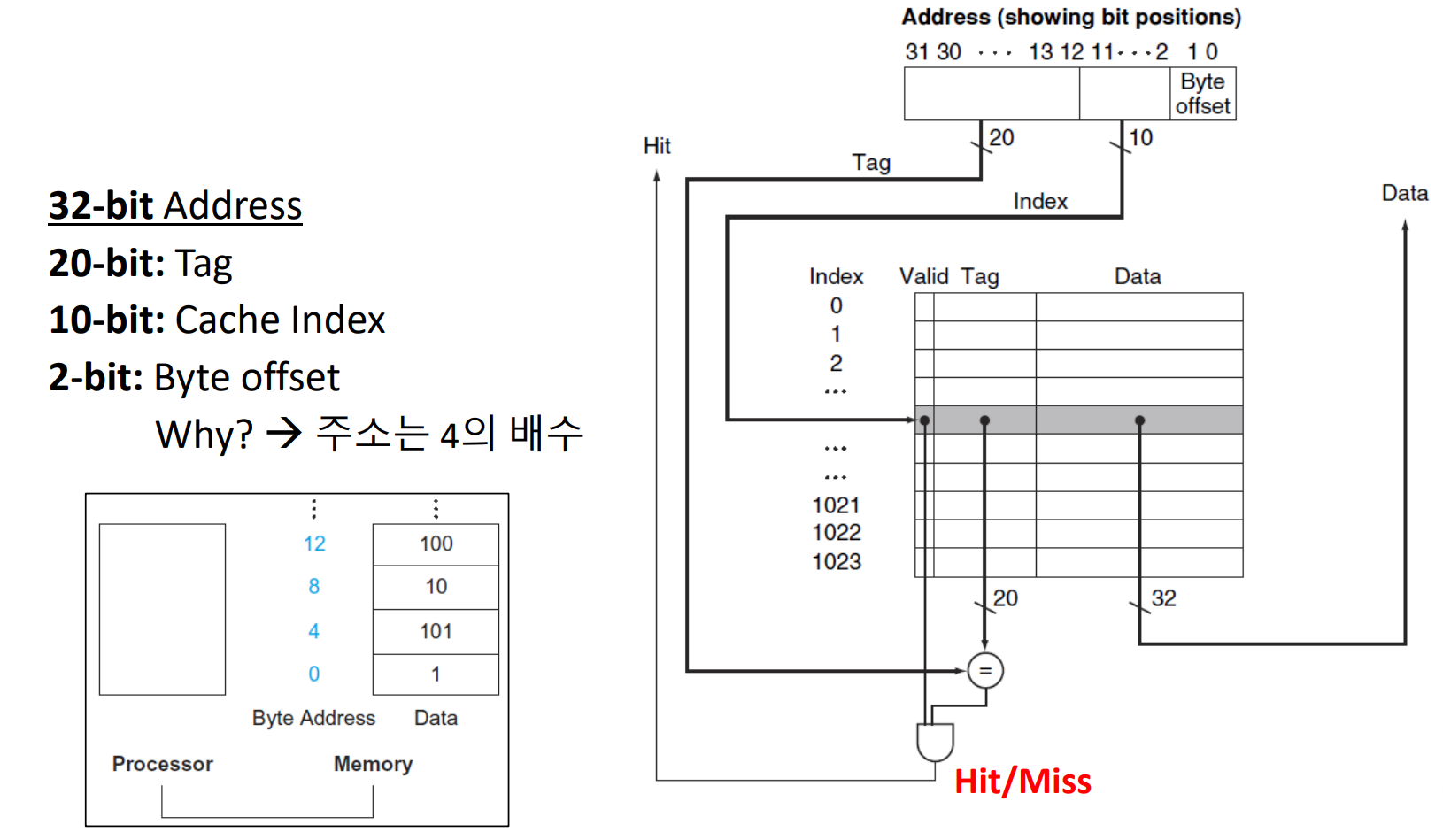
▶ 1 word block
address는 byte addressing 기법을 사용하기에 0, 4, 8, .. 이런 식으로 4의 배수로 만들어 주어야 한다.
때문에 이런 식의 접근을 위해 byte offset은 항상 00이다.
Tag = Address (32-bit) - Cache index (10-bit) - Byte offset (20-bit)
Tag bit은 처음부터 정의한 것이 아니라 나머지 부분에 할당되는 개념이다.
Hit process
1. cache index로 이동
2. 해당 index에 대한 block의 valid bit = 1 확인, tag bit 같은지 확인 - and gate
3. CPU에 전달
※ 위 예시에선 cache index의 크기가 10-bit이기에 2^10개의 word를 저장할 수 있다고 가정한다.
Larger block size
spatial locality에 의해 하나의 값을 가지고 오면 주변에 있는 값들을 부를 확률이 높다.
때문에 block size가 커지면 커질수록, 즉 word의 개수가 많으면 많을 수록 다시 main memory에 접근할 필요가 없어,
속도가 빨라진다는 장점이 있다.

▶ Lager block size
※ byte offset: 2-bit 고정
만약 block offset과 cache size의 자리를 바꾸면 어떻게 될까?
block offset: 한 번에 가지고 올 bit 수
원래는 block offset에 byte addressing이 적용된, 즉 4가 곱해진 형태인데
만약 block offset과 cache size의 자리를 바꾸면 offset + cache size만큼 block offset(size)가 커져
0, 4, 8, .. 단위로 움직이던 것이 256, 512, 768, ... 단위로 움직이게 되어 spatial locality가 깨지게 된다.
즉, block offset을 MSB 쪽이 아닌 LSB 쪽에 두는 이유는 주변 값을 뭉탱이로 가지고 오게 하기 위해서이다.
16 KiB data and 4-word blocks일 때, direct-mapped cache에 필요한 total bits 수는?
※ KiB = 2^10 byte, assume: 32-bit address
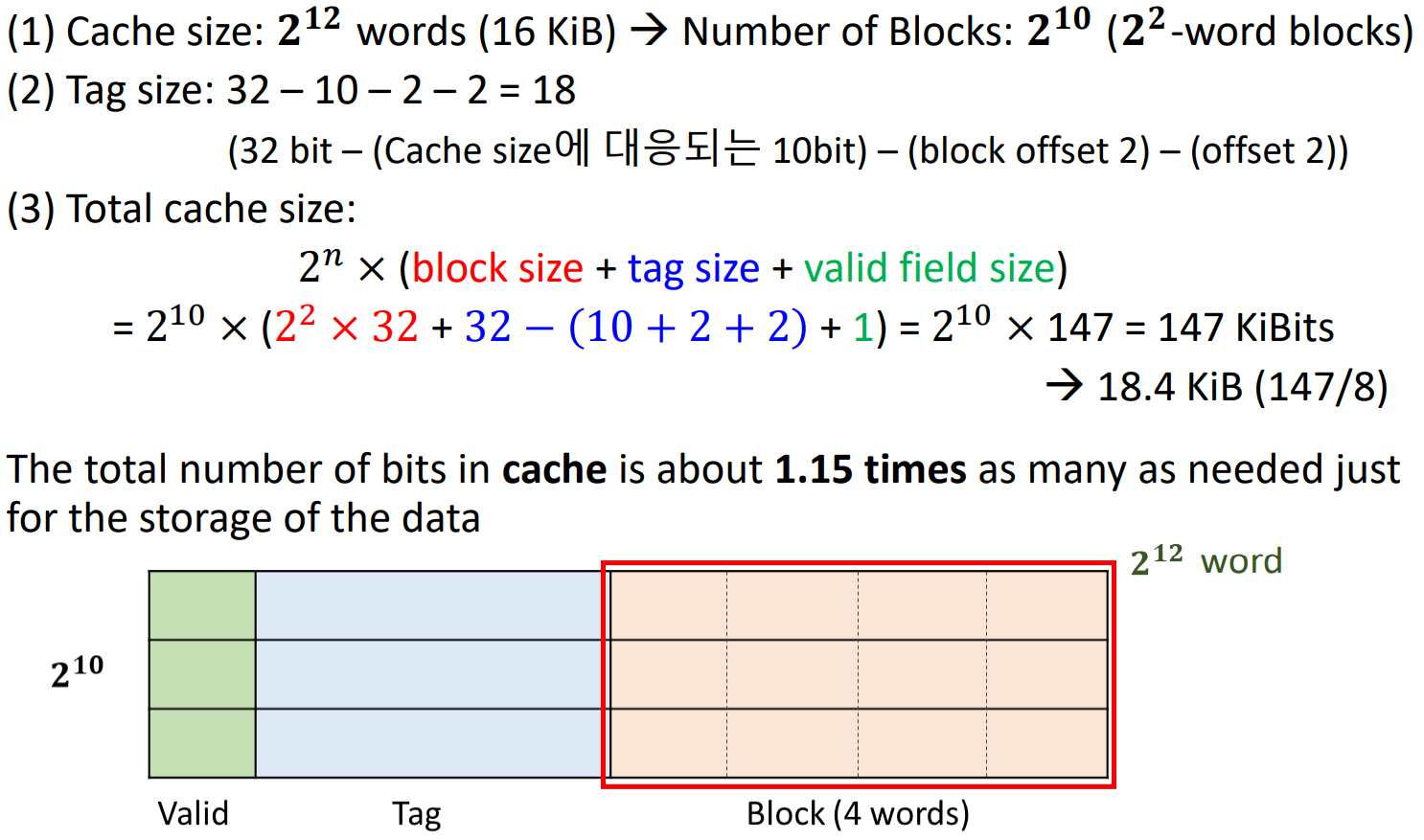
▶ 8-bit = 1-byte
- 2^12 words (16 KiB)인데, block당 word 개수가 2^2 -> block의 총 개수(Cache size)는 2^10 (= 2^12 / 2^2)
- word blocks = 2^2 -> block offset = 2
※ bit를 byte로 변환시에는 8 차이가 나기에, 8로 나누어 주어야 한다.
cache memory는 data만 저장하는 게 아니라, tag와 valid bit도 저장한다.
때문에 하나의 cache index에서 필요한 bit 수는
- block size 2^m word 개수 × 32개 (데이터 bit 수)
- tag bit (32 - n - m - 2)개
- valid bit 1개
여기서 word 개수에 32를 곱해주는 이유는 하나의 word가 32bit이기 때문이다.
이때 하나의 word는 32-bit, 즉 4-byte이므로, 2^m word = 2^(m + 2) byte이다.
16 KiB = 16 × 2^10 byte = 2^14 byte
4-word blocks: 1 block = 4 words
이때 4-byte가 1 word이기에, 16 KiB = 2^(14 - 2 ) words = 2^12 words이므로, 2^12개의 데이터를 저장할 수 있다.
2^2개의 word block을 저장하기에 cache block, 즉 cache의 index 수는 2^10개로 index 표현 bit 수는 10 bit이다.
때문에 Tag bit = 32 - 10 - 2 - 2 = 18으로,
전체 필요한 cache size = 2^10 × (2^2 × 32 + 18 + 1) 이다.
-> 16 KiB에 데이터 저장을 위해서는 18.4 KiB 만큼의 bit 수 (cache size)가 필요하다. 즉, 2.4만큼의 오버헤드가 발생한 것이다.
오버헤드가 발생한 이유는 데이터뿐만 아니라 tag bit, valid bit이 필요하기엥 추가적인 오버헤드가 발생하는 것이다.

▶ Larger block size (16 words / Block)
16 words / Block -> m = 4
16개의 32-bits, 즉 16개의 데이터 중 각 word를 mux에 입력으로 넣어 그 중 필요로 하는 데이터를 찾는다.
이때, block offset을 통해 주소를 보면 필요로 하는 데이터인지 알 수 있다.
cache가 64개의 block으로 이루어지고 block size는 16 byte일 때,
byte address 1200은 어떤 block number에 매핑될까?
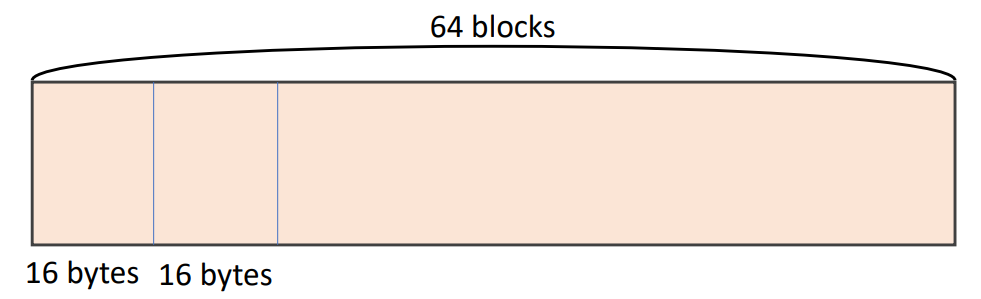
▶ Example

▶ Block address
이때, block address가 75가 나오는 1200 ~ 1215는 모두 같은 cache memory 위치에 저장된다.
(Block address) modulo (Number of blocks in the cache)
-> 75 modulo 64 = 11
Miss Rate vs. Block Size
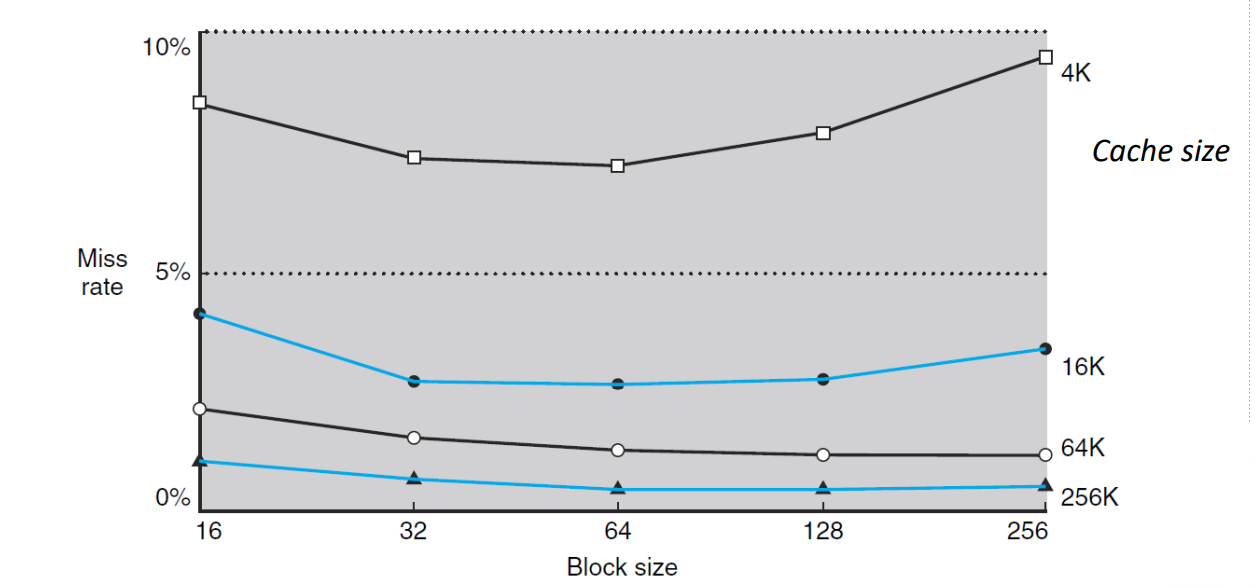
▶ Miss Rate vs. Block Size
Cache size (4K, 16K, 64K, 256K)가 클수록 임시적으로 저장할 수 있는 데이터가 많아지기에,
즉, spatial locality에 의해 miss rate이 감소한다.
또한, cache size가 작아지면 작아질 수록 저장할 수 있는 공간이 적어지기에 자주 교체가 된다.
그러므로 temporal loclaity도 이에 해당한다.
Block size가 커질 수록 spatial locality에 의해 miss rate은 감소한다.
그러나, 일정 구간 부터는 block size가 너무 증가함으로써 다양한 block들을 가져오지 못하는 문제로 인해, miss rate이 증가한다.
이는 cache size가 작을 때 두드러진다.
그 이유는 적은 데이터를 저장할 땐 다양성이 없어진 게 확연히 눈에 띄지만, 커질 수록 그런 현상이 두드러지지 않기 때문이다.
Handling Cache Misses

▶ Handling Cache Misses
1. Original PC
- original PC 값을 memory에 전송
2. Read PC
- main memory에 read를 수행하도록 지시하고, memory가 접근을 완료할 때까지 대기
3. Writing
- memory에서 가져온 data를 cache entry의 data 부분에 저장
- address의 upper bits를 tag field에 writing
- valid bit on
4. Refetch
- 첫 번째 단계에서 instruction을 refetch하여 instruction 실행 재시작
- 즉, cache memory에 저장된 값을 CPU에 전달
- 이때는 cache에서 instruction을 찾을 수 있음
Handling Writes
Handling writes

▶ Handling writes
- store word instruction에서 data를 cache memory에만 write 했다고 가정
- cache에 data를 write한 이후, main memory는 cache memory와 다른 값을 가지게 됨
- 이런 경우, cache와 memory가 inconsistent(차이 발생)라고 함
-> cache memory의 업데이트된 값을 memory로 옮겨야 한다.
1. Write-through

▶ Write-through
- main memory와 cache memory의 consistent를 유지하는 가장 간단한 방법은 data를 항상 main memor와 cache memory에 동시에 쓰는 것임
- 즉, cache memory에 sw 하자마자 main memory와의 차이가 생기기 전에 main memory에도 업데이트해 주면 됨
- 이를 통해 main-cache 간의 데이터가 항상 consistent
- 그러나, 좋은 성능 (속도) 제공하지 않음 (cache의 존재 이유가 없어짐)
2. (Write-through) Use Write buffer
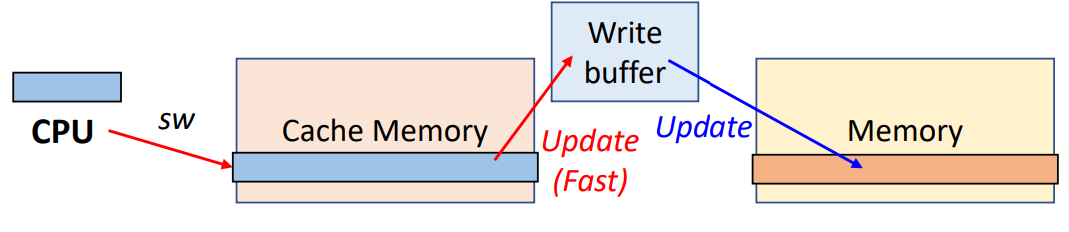
▶ Use Write buffer
- Write Buffer는 data를 memory에 write하기를 기다리는 동안 저장하는 역할을 함
- data를 cache와 Write Buffer에 write한 후, processor는 실행을 계속 진행할 수 있음
- 이렇게 write buffer에 차곡차곡 쌓다가 일정 순간에 main memory로 업데이트
- main memory에 write가 완료되면 Write Buffer의 entry는 freed
- processor가 write에 도달했을 때 Write Buffer가 가득 차 있다면, Write Buffer에 empty position(빈 자리)이 생길 때까지 processor는 Stall
3. Write-back

▶ Write-back
- Write이 발생할 때, 새 값은 cache memory에 있는 block에만 write됨
- 수정된 cache memory의 block은 block이 교체될 때 main memory에 write됨
- Dirty bit: cache에 있는 data가 업데이트되었는지(Dirty) 업데이트되지 않았는지(Clean)를 나타내는 indicator (1-bit)
- 즉, 교체될 때 dirty bit가 1이면 main memory에 저장
- memory access efficiency를 향상시킴 (성능 개선)
- 가장 현명한 solution임
'CS > 컴퓨터 구조' 카테고리의 다른 글
| Lecture 19: Memory Hierarchy - 3 (0) | 2024.12.15 |
|---|---|
| Lecture 18: Memory Hierarchy - 2 (1) | 2024.12.15 |
| Lecture 16: The Processor - 5 (2) | 2024.12.06 |
| Lecture 15: The Processor - 4 (0) | 2024.12.03 |
| Lecture 14: The Processor - 3 (1) | 2024.12.01 |